マーケティング用語集
平均値
データの総和をデータの個数で割ったものを平均値(mean)という。
平均値の求め方
ある製品ブランドXについて、調査対象者10名の年間購入量がそれぞれ以下の通りだったとする。
| Aさん | Bさん | Cさん | Dさん | Eさん | Fさん | Gさん | Hさん | Iさん | Jさん |
|---|---|---|---|---|---|---|---|---|---|
|
3個
|
4個
|
6個
|
4個
|
5個
|
3個
|
2個
|
4個
|
5個
|
6個
|
このとき、製品ブランドXの年間購入量の平均値は以下の計算式で求めることができる。
平均値=(3+4+6+4+5+3+2+4+5+6)/10=4.2
エクセルで計算する場合には、AVERAGE関数を使用することで、「=AVERAGE(範囲)」で簡単に求めることができる。
平均値を使う際の注意点
平均値は、データを要約して捉えることができ便利だが、データに極端に小さな値や大きな値(外れ値)が含まれているとき、その影響を受けてしまうため注意が必要。
例えば先ほどの例で、10名のうち一人(ここではJさんとします)の年間購入量が極端に多く、40個だったとする。
| Aさん | Bさん | Cさん | Dさん | Eさん | Fさん | Gさん | Hさん | Iさん | Jさん |
|---|---|---|---|---|---|---|---|---|---|
|
3個
|
4個
|
6個
|
4個
|
5個
|
3個
|
2個
|
4個
|
5個
|
40 個
|
その場合、製品ブランドXの年間購入量の平均値は、以下の計算式から、7.6個となる。
平均値=(3+4+6+4+5+3+2+4+5+40)/10=7.6
しかし、あらためてデータを見てみると、10名の中で年間購入量が7個以上なのはJさんのみで、それ以外の9名は2~6個に分布しており、この10名の年間購入量を要約した値として7.6個というには違和感がある。このような場合には、要約した値として平均値以外の代表値(中央値や最頻値)を使うことや、特にデータの異常・取得時のミスが疑われる場合にはトリム平均(データの上下数%を除外して算出する平均値)を使うことなどを検討する必要がある。
下図のように、データの分布が左右非対称であるときにも、平均値がひっぱられてしまうため注意が必要。

また、下図のように、データの分布の山が二つある場合(二峰性の分布)も、平均値で要約することが難しく注意が必要。
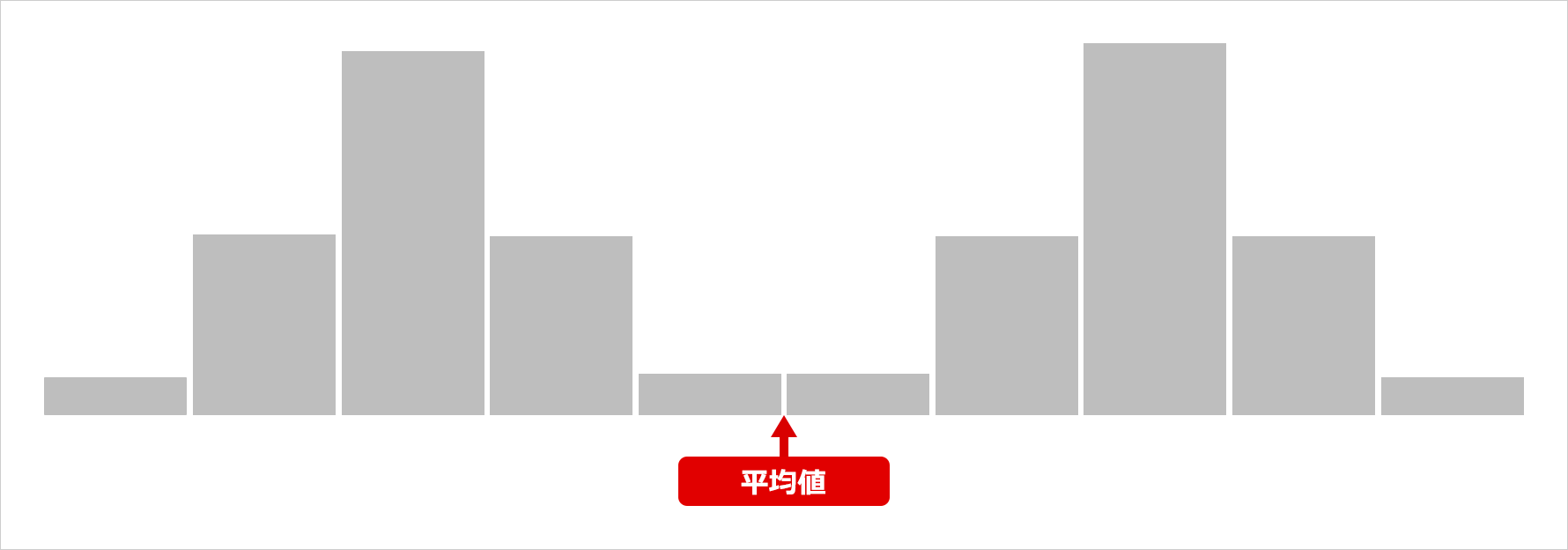
平均値以外の代表値
平均値以外の代表値には、以下のようなものがある。
中央値(median)
データを大きさの順に並べたときに、真ん中にくる値を中央値という。データの数が偶数のときは、真ん中にくる2つの値を足して2で割ったものが中央値となる。
最頻値(mode)
データの中で、もっとも頻度が高い値を最頻値という。
