マーケティング用語集
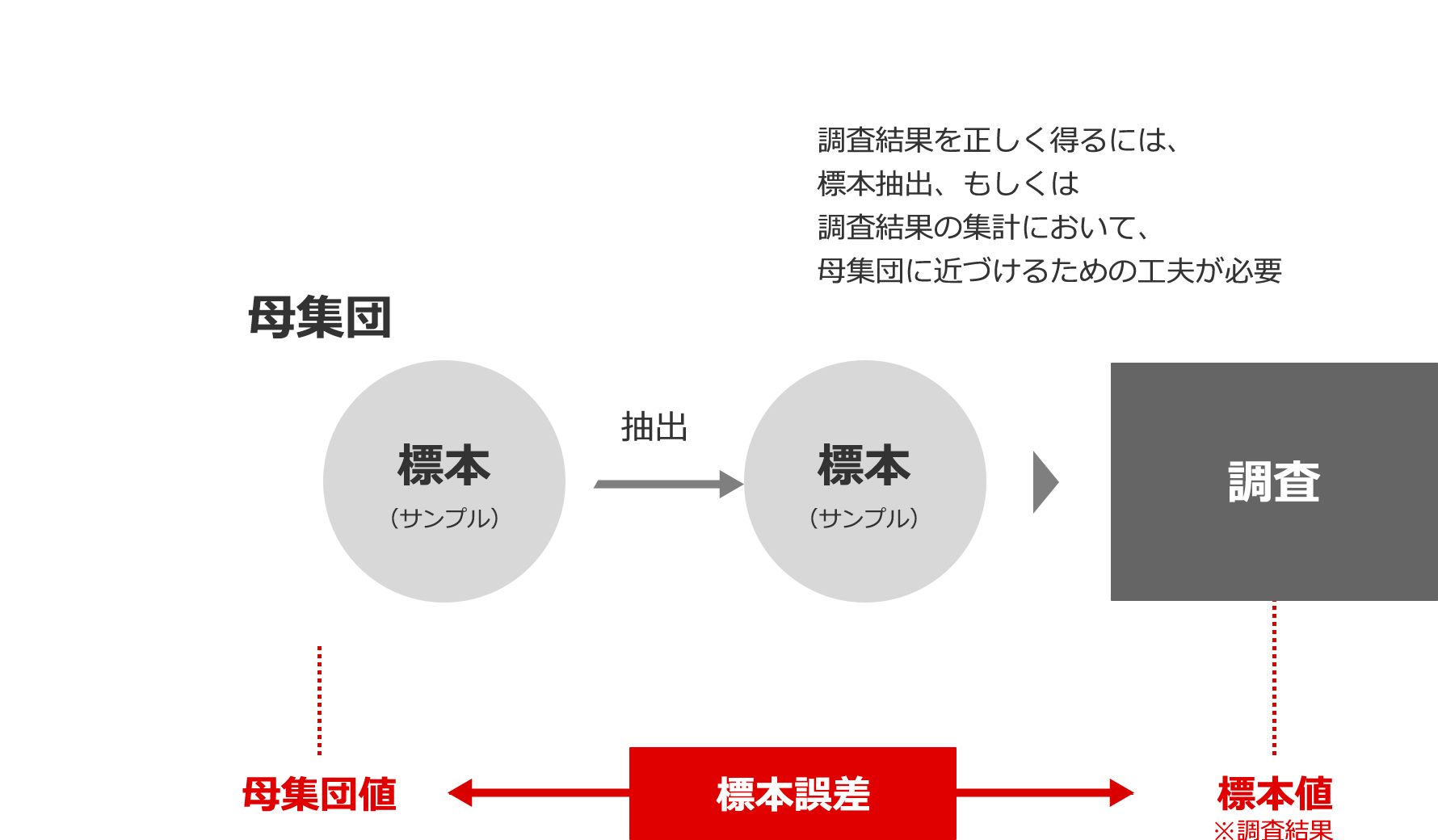
標本誤差
標本調査(母集団から一部の標本を抽出して行う調査)を行って母集団値を推定する際に生じる、標本値と母集団値との差。
この誤差がどの範囲の大きさで生じるかは、確率論に基づいて一定の式で計算することができる。標本誤差は抽出数を多くするほど小さくなり、また母集団内での個別データのバラツキが小さいほど小さくなる。
標本誤差はデータ利用者にとっての保証
調査結果の数字はふつう平均値や比率(パーセント)で表される。したがって、標本値を調査から得られた平均値や比率とすると、それらが母集団値とどれだけ食い違っているかは
「標本誤差」=「標本値」ー「母集団値」
として定義される。しかし母集団値は未知であり、標本値も抽出される標本によって左右されるため、標本誤差の大きさそのものを示す式とはならない。個々の標本誤差はわからないが、その範囲は「標準誤差」という統計値を用いて確率的に記述できる。それがデータの利用者にとって調査結果の信頼性の保証となり、平均値なり比率なりを安心して使える限界を知らせてくれることになる。
平均値の標準誤差

単純な無作為抽出法では、平均値mの標準誤差を次式で計算できる。(σmは平均値の標準誤差、nは調査対象数、σは母集団の個別データの標準偏差(調査データから推定))
この値を用いて「標本平均の前後に標準誤差の1.96倍の幅をとると、母集団平均がその中に入る確率は95%である」と言い切ることができる。この範囲のことを信頼区間と呼び、その中に入る確率を信頼係数と呼ぶ。また、標準誤差の2.58倍の幅をとれば、信頼区間を99%にすることができる。
比率の標準誤差

比率pの標準誤差は次式で計算できる。(母集団における比率Pは不明なので標本値pで代用(nがある程度大きいとき))
もし調査対象者数が400人でその中の20%がある製品の使用者であったとすると、使用率の標準誤差は2%と計算することができ、母集団における使用率が区間16~24%内にあることが確率95%で保証される。
標本誤差早見表
- 比率が50%に近づくほど、標本誤差は大きくなる。
- サンプルサイズが大きくなるほど、標本誤差は小さくなる。
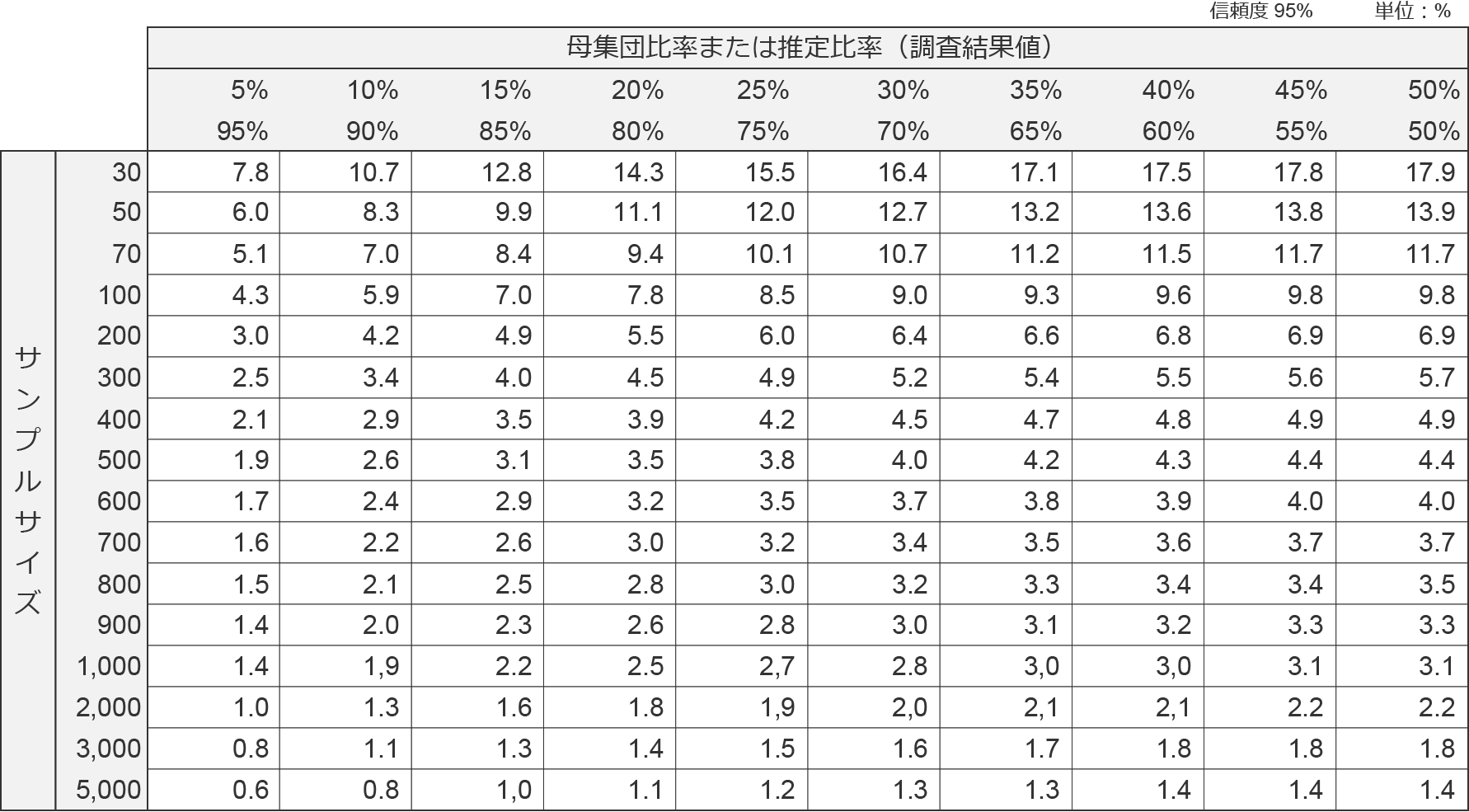
※インターネット調査は厳密な標本調査ではないが、標本誤差の考え方を活用して判断するケースが多い。
関連資料
定量調査の全体の流れを知りたい方に向けたお役立ち資料
i-Guide はじめてのマーケティングリサーチ リサーチの基礎 編 はこちら
