数量化理論

統計学者の林知己夫氏によって開発された手法で、市場調査においても広く適用されている。
その理論はやや難解なため、ここでは一般的な意味での「数量化」の考えから解説する。

スコアを与える

ある製品テストを考える。いま、試作品AとBがあり、それぞれを試用させて評価を次の5段階カテゴリーで回答してもらうものとする。

• 非常によい
• まあよい
• ふつう
• あまりよくない
• 全くよくない

この方法を用いてあるまとまった人数についてテストを実施して、どちらの製品がすぐれているかを判定するとき、もしA製品には「非常によい」「まあよい」という回答が多く、B製品には「ふつう」「あまりよくない」が多いとすると、判定は「A製品のほうの評価が高い」とすることに異存はないと思う。
しかし、2つの製品の優劣が接近していると、このような回答分布の比較ではうまくいかなくなる。そこで上の5段階に順に5点、4点、3点、2点、1点のスコアを与えてみると、回答分布から平均スコアを計算することができる。もしA製品が平均4.2、B製品が平均3.8を得たとすれば、差引0.4だけ前者のほうが高く評価されたという結論になり、一連のカテゴリーにこのようなスコアを与えることで、その項目を一つの変数に変換し、こまかな比較計算が可能となる。

製品属性による「おいしさ」の説明

しかし、どのような状況においても、上のようにカテゴリー順に等間隔のスコアを与えればよいというわけではない。
たとえば、たいていの嗜好飲料はほどほどの甘味であればおいしく、冷たいか熱いかどちらかで生ぬるいのはおいしくない。そこで「おいしさ変数」はそのままにしておき、それを「甘味の度合」と「温度」との変数を用いて簡単な1次式で表そうとした場合、単純に「甘味が強い」「ほどほど」「甘味が足りない」に3点、2点、1点を与え、「熱い」「ぬるい」「冷たい」に3点、2点、1点を与えたのではうまくいかず、工夫が必要になる。

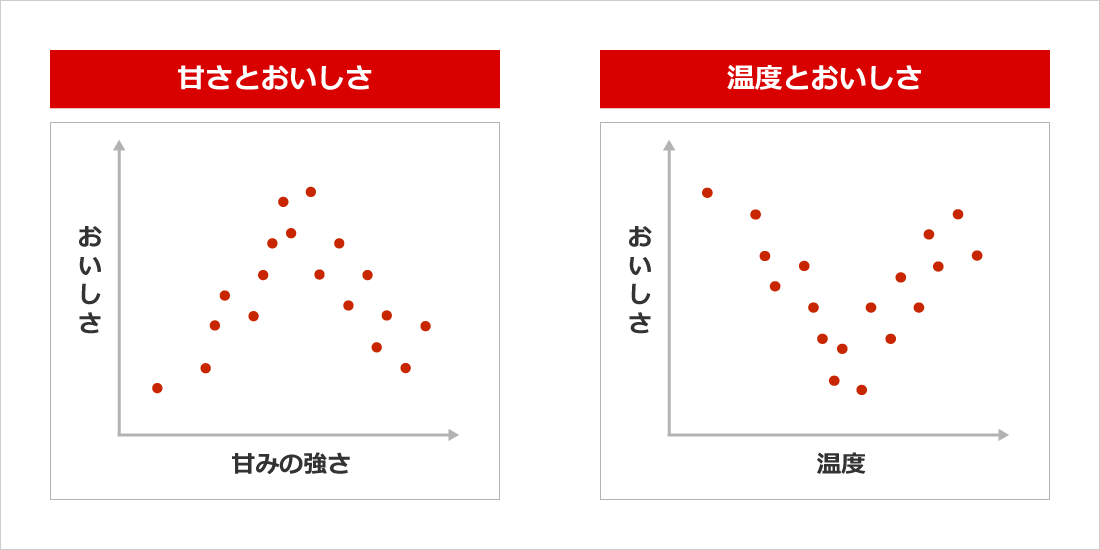
上の単純な方法は「おいしさ」という目的変数と「甘味の度合」および「温度」という2つの説明変数による「重回帰分析」にほかならない。そして、“工夫”が今回のテーマである「数量化理論」による手法である。甘味と温度のすべてのカテゴリーにそれぞれ適切なウエイトを与えることによって、1次式による計算値が「おいしさ変数」のスコアに一致するようにするのである。

他手法と数量化理論との対応関係

数量化理論とは、いくつかの調査項目を無理に1つの変数として扱わないで、カテゴリーに分解してその一つ一つに適切なウエイトを計算して与える方法であると理解できる。この理論はいくつかの手法群に分かれていて、それぞれが他の手法と対応関係にある。
前項の事例は「重回帰分析」に対応する「数量化1類」。そのほかに「判別分析」に対応する「数量化2類」、「主成分分析」または「因子分析」に対応する「数量化3類」がある。