マーケティング用語集
重回帰分析
統計学上のデータ解析手法のひとつ。
統計用語で「重」は「複数」、「回帰」は「因果関係」を意味する。つまり重回帰分析とは、ある結果(目的変数)を説明する際に、関連する複数の要因(説明変数)のうち、どの変数がどの程度、結果を左右しているのかを関数の形で数値化し両者の関係を表し、それを元にして将来の予測を行う統計手法のこと。
たとえば小売業で、10店舗ある既存店の売場面積、従業員数、販売商品数、駐車場の収容台数、駅からの距離など複数の要因が、売上高という結果をどの程度決定づけているのか分析し、出店予定の新店舗の各変数から、将来の売上高を予測するといった場合に利用される。
応用範囲が広く、要因と結果という関係を定式化しマーケティング施策の効果測定が出来ることから、売上予測や、プロモーション戦略策定などマーケティングの現場で使われることの多い手法である。
単回帰分析と重回帰分析
回帰分析では、さまざまな要因の間にどのような関係があるのかを分析する。たとえば広告費から売上を予測する。このように1つの要因から結果を予測することを「単回帰分析」と呼ぶ。
具体的には、広告費をいくらにしたら売上がいくらになったという実績データを数多く集め、両者の関係を「回帰係数」という数字で表す。
●単回帰分析のモデル

●単回帰分析の散布図
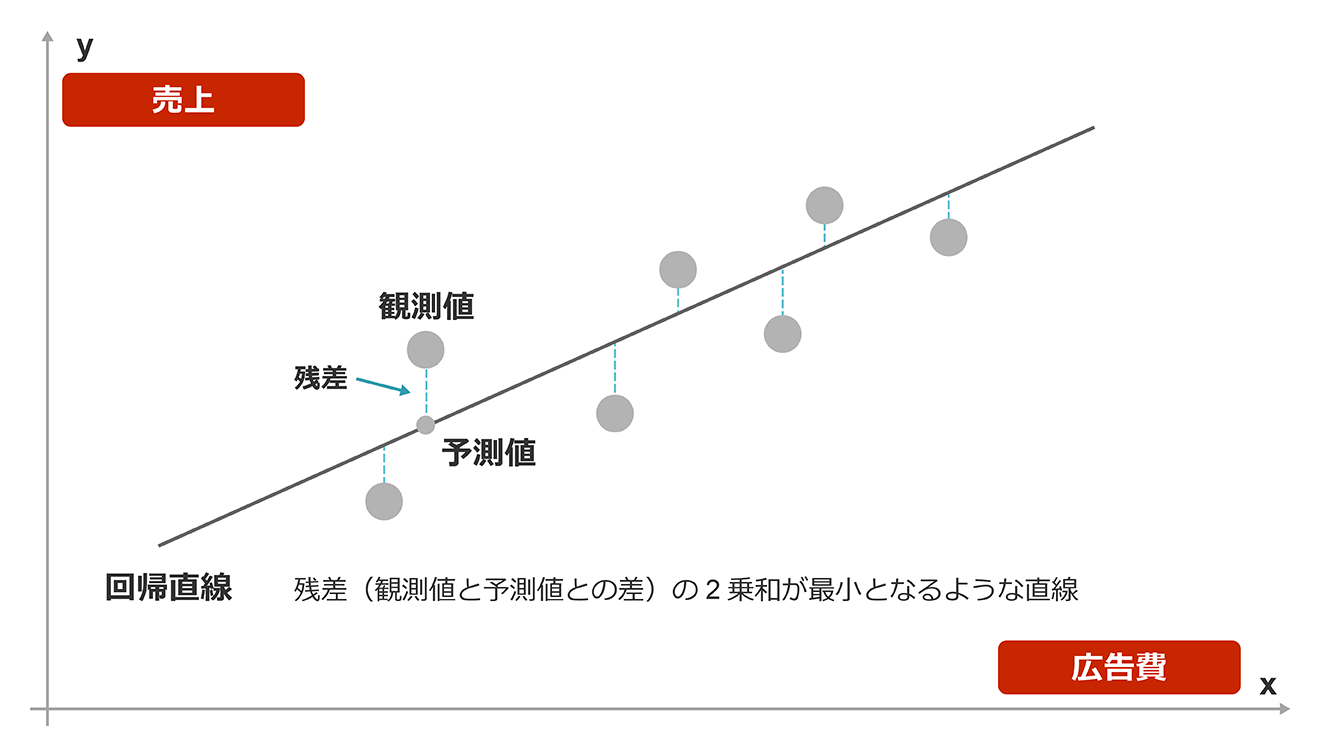
説明変数を広告費など単一の要因だけではなく、より増やして売上を予測するのが、「重回帰分析」である。
◎重回帰分析のモデル
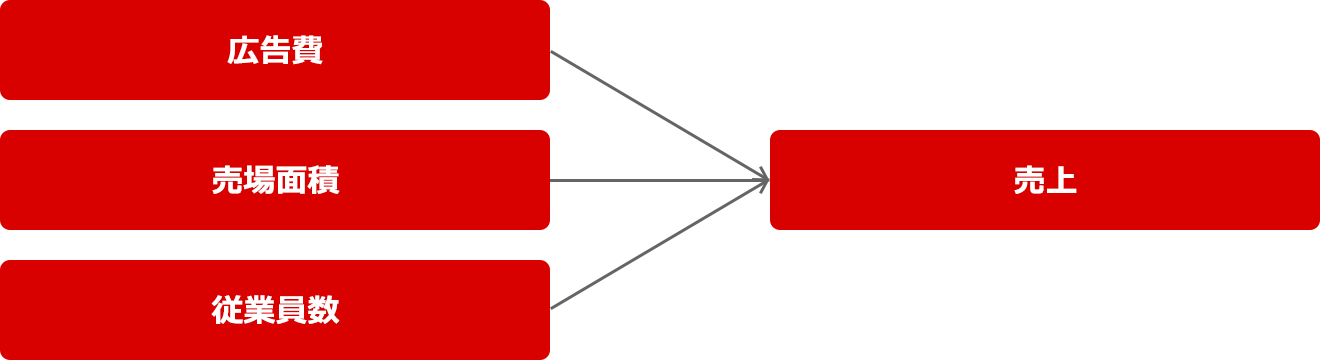
通常、ビジネスの現場では重回帰分析が使われることが多いが、たとえば大きな広告キャンペーンを開始する前に、これまでの広告費だけを変数に単回帰分析を実施し、認知率や売上を予測するといったことも行われる。
重回帰分析の手順
重回帰分析は、変数間の相関関係から、目的変数と説明変数の関係を「重回帰式」という方程式で表す作業。その手順を、例を挙げて見ていく。
Step1/分析対象となる成果(目的変数)を決める
郊外に10店舗のレストランを経営する会社の企画室に配属されたAさんは、オープン予定の新店サポートを指示され、KGI(重要業績評価指標)となる売上高を予測することに決めました。
Step2/成果を左右する要因(説明変数)を考える
店舗の売上高に関連を与えそうな要因は数多くありますが、Aさんはその中でも、特に重要で、既存店のデータを揃えられそうな説明変数の候補をピックアップしました。

Step3/データを収集し、統計ソフトで解析
Aさんは社内の各部署から、上でピックアップした説明変数のデータを集めました。数字データ(量的変数)以外のデータ(質的変数)がある場合、1と0の二者択一式に変換したダミー変数を作成しました。この例では「性別」で、男性=0・女性=1に変換して、性別による影響を調べることになる。
そして、エクセルの分析ツールで重回帰分析を行っていきました。無料のフリーウェア「R」や、企業や学術・研究機関では「JMP」や「SPSS」といった有料ソフトもよく利用されています。
候補となる説明変数をひとつひとつ加えたり、減らしたりしながらデータの精度を高める「ステップワイズ法」で最適な組み合わせを探っていきました。説明変数の個数は多すぎても少なすぎても良い分析結果は得られません。数は7個程度という場合が多いようです。
試行錯誤の結果、自社店舗の売上高は、下の6個の説明変数によって説明するのが最も適切だとわかりました。
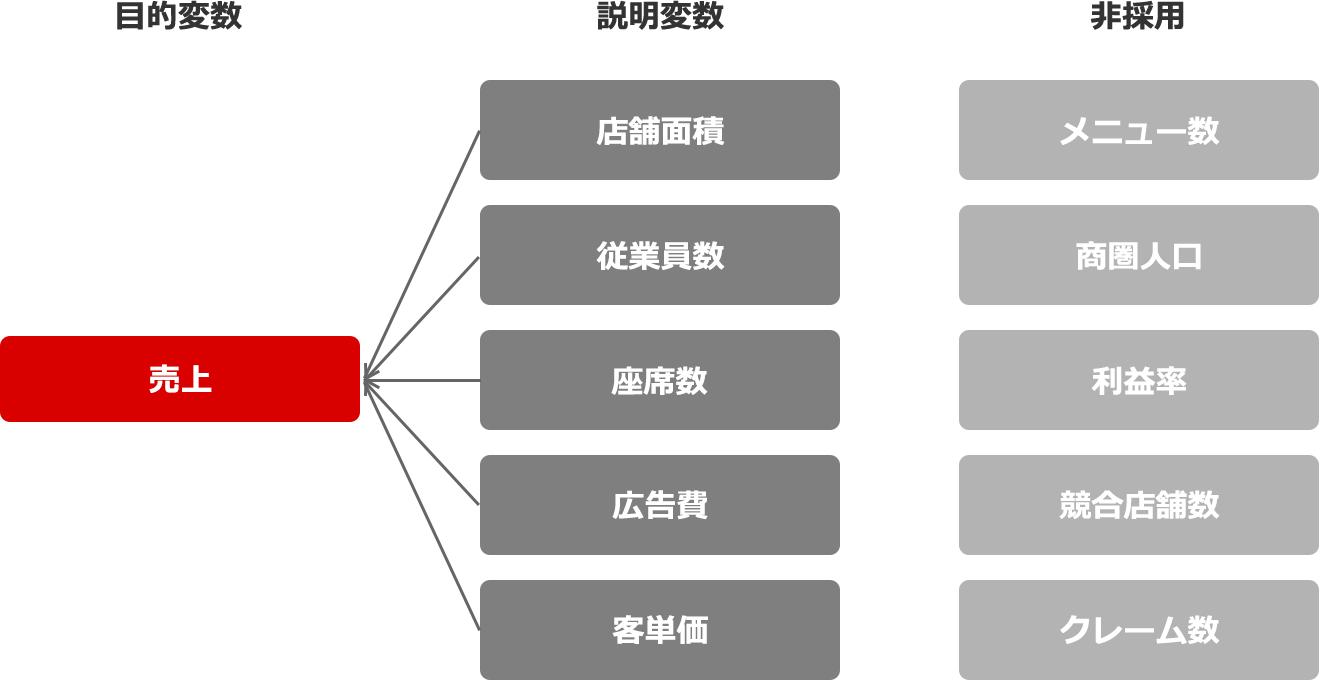
Step4/重回帰式が完成
そうして割り出された重回帰式は、このような方程式となる。

「回帰係数」は「偏回帰係数」とも呼ばれるが、大きさが変数の単位に依存するためその数字自体にあまり意味はなく、ある要因に比べて他の要因の係数が大きいからといってその要因の売上額への影響が大きいというわけではありません。影響度の大きさは一般的に、解析ソフトで出力される「標準化係数」という数値を使う。
標準化係数は、ある要因が目的変数に対して与える影響の大きさを数値化したものです。重回帰分析で扱う各要因は、たとえば店舗数(単位:店)、広告費(同:千万円)、客単価(同:千円)など、様々な単位の数値がありますが、それらの影響が単位に左右されることなく比較できるように係数化したものです。
標準化係数以外には、「寄与率」や「寄与度」という数値を算出して影響の大きさを比べる場合もある。
「定数項」とは「y切片」とも呼ばれ、説明変数が変わっても固定されたままの値のことを指す。この例では、店舗面積など各説明変数によって変動しない、売上高の「ベース」を意味する。
Step5/新店売上高を予測し、対策を施す
Aさんは重回帰式に新店の計画データを入れてみました。すると、目標より低い数値になってしまいました。そこで、採用した6個の説明変数の寄与率を計算したところ、想定より従業員数の影響が大きく、広告費の影響が小さいことがわかりました。Aさんは次の経営会議でデータを基に予算配分の変更を提案することに決めました。
以上が、重回帰分析の基本的な手順例になる。
重回帰分析は「多変量解析」の一手法
重回帰分析は、マーケティングにおいて頻繁に使われる「多変量解析」のための分析手法のひとつ。多変量解析とは、複数の変数を持つデータの関連性を明らかにする統計手法のことで、重回帰分析以外にも、多くの分析手法がある。解析の目的や、扱う対象となるデータの種類によって、表のように分類できる。
●多変量解析の主な分析手法
|
分析の目的 |
目的変数 | 説明変数 | |
| 量的変数 | 質的変数 | ||
|
予測 |
量的変数 |
|
|
| 質的変数 |
|
|
|
|
要約 |
なし |
|
|
多変量解析の目的は大きく分けて、購入率、売上や当選率など何らかの結果を「予測」することと、学校の試験結果を文系と理系に集約するなど「要約」することの二つに分けられる。さらに扱うデータが数字による量的変数か、性別などの数字ではない質的変数かによって解析手法が異なる。
それぞれを簡単に解説する。
重回帰分析
複数の量的な説明変数から、一つの目的変数を予測する手法。たとえば、店舗面積・従業員数・商圏人口・広告費から、来客数を予測するといった分析。
数量化Ⅰ類
基本的には重回帰分析と同様ですが、質的変数から量的変数を予測する分析手法。たとえば、性別、飲酒の有無、喫煙の有無、運動の有無から、癌になる確率を予測するといった分析。
判別分析
上の数量化Ⅰ類と逆で、量的変数から質的変数を予測し、1か0のグループ分けをする手法。たとえば、B2Bビジネスにおける見込み客の企業規模・従業員数・売上高・利益率から、契約/非契約を予測するといった分析。
ロジスティック回帰分析
判別分析と似ていますが、1か0かを判別するのではなく、目的変数が1となる確率を予測する手法。たとえば、見込み客の企業規模・従業員数・売上高・利益率から、その見込み客が契約する確率を予測するといった分析。
数量化Ⅱ類
判別分析と同様、グループ分けする分析手法ですが、質的変数から質的変数を予測する。たとえば、性別、飲酒の有無、喫煙の有無、運動の有無から、癌になる/癌にならないなどの予測をするといった分析。
主成分分析
複数の量的な説明変数を、より少数の主成分という指標(合成変数)に要約・集約する分析手法。たとえば、学校で10科目の試験を行った際、第1主成分で総合得点という1つの指標に要約し、第2主成分で文系得点/理系得点という2つの指標に要約するといった分析。
因子分析
主成分分析は複数の説明変数を素に、少数の変数を作成しますが、因子分析は複数の説明変数に影響を与えている共通因子を抽出する分析手法。たとえば、学校の10科目の試験結果のうち、現代国語と古文と論文の成績が良いのは、文系因子が高いからだと説明するといった分析。
クラスター分析
異なる性質の人や物が数多く集まっている集団から、何らかの視点で似た性質のクラスター(集団)を集め、グループ分けする分析手法。たとえば、従業員アンケートの結果から、マイペース型と集団型を分けたり、ファッション感度の高いクラスターを抽出したりするといった分析。
数量化Ⅲ類
主成分分析と似た手法で、複数の質的な説明変数から少数の変数へと要約する分析手法。たとえば、顧客アンケートを元に、商品やブランドのポジショニングを分類するといった分析。
コレスポンデンス分析
数量化Ⅲ類と同様の手法で、クロス集計表などの量的な説明変数を用いたものを指す。たとえば、顧客アンケートの結果をクロス集計して、商品やブランドのポジショニングを分類するといった分析。
※解説に使用しているデータ、図版はダミー
