マーケティング用語集
時系列分析
時系列データの変動
時間の単位としては、日別、週別、月別、期別、年別がある。その時間単位ごとの売上や、価格が時系列データ。横軸に時間を取り、縦軸に時系列データをとって折れ線グラフまたは棒グラフであらわすと、ある商品について売上、価格がどのように変化したか一目でわかる。「ここ2、3年は順調に売れている」、「夏場は多く売れ、冬場はあまり売れない」、「売上と価格に関係がある」といったことがわかる。
長い期間の大まかな傾向は「長期変動」または「トレンド」と呼び、季節によって同じような増減サイクルがあればそれを「季節変動」と呼ぶ。またあるブランドが広告キャンペーンをしたり、ある店が「在庫一掃セール」をしたり、そのほか理由のはっきりしない変動があるとき、これらの原因を合わせたデータのばらつきを「不規則変動」とする。
時系列データの分解
時系列データはこれら異なる変動要因を組み合わせたものとして、次のようなモデル式で表現される。

この式はかならずしも足し算形式でなくてもよく、各変動のかけ算でもよいし、両形式の組合せでもよいとされる。
時系列分析というとき、その目的は上式に含まれる変動要因の分解になる。分解の仕方は市販のソフトでプログラム化されていますので、誰でも容易にできる。
時系列分析による予測
過去のある期間の年別データがあって、それを用いてこれから先を予測することを考える。
いま、売上「X」を時間(年)「t」で表す式として次の1次式を想定する。

式中の未知のパラメータ「a」および「b」は過去の売上データから計算することができる。この式は「a+b×t」のトレンド部分と、「e」の不規則変動部分に分解していることを表している。
この分解が妥当であれば、時間「t」を大きくすることによって、トレンドの延長として売上「X」の予測値が計算できる。式の不規則変動「e」は先々不明なので、予測計算には入れない。
予測のための条件
前項の予測方法における前提は、トレンド計算に用いた過去のデータ条件が引き続きそのまま予測期間中も存続している。
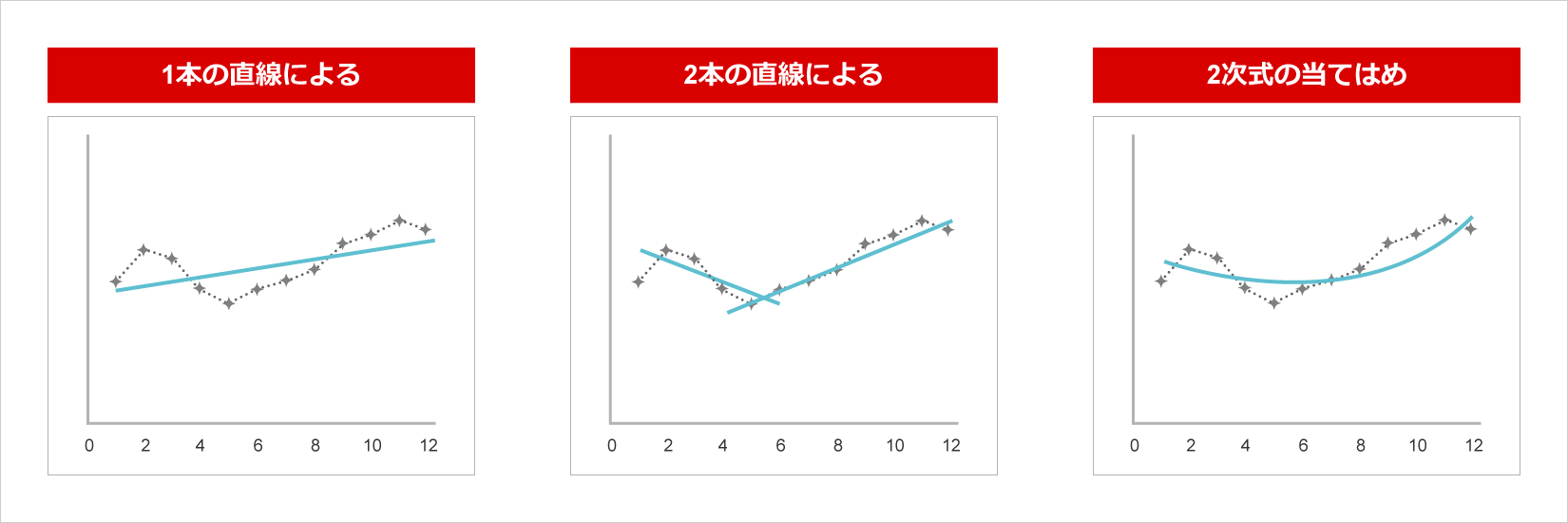
図の時系列データ例は最初の何年かが減少傾向、あとは最近年まで増加傾向。ここでトレンドの求め方として、次の3通りを考えてみる。
(a)図は1本の直線でトレンドを表しているので、この線の上下にはみ出した分は不規則変動とみなされる。この直線は傾斜がゆるやかなので延長しても予測値はそう大きくなりません。
(b)2本の直線でトレンドを表していて、予測に利いてくるのは増加傾向を示すあとのほうです。したがって予測値はその延長としてより大きくなりそうです。
(c)曲線(2次式)を当てはめているので、時間「t」が大きくなるほどその自乗の項が利いて、予測値は今後急激に増大する。 どの予測結果がよいでしょうか?結果を判断する一つの基準として、過去データの変動をどれだけ説明できているか(当てはまりがよいか)がある。