マーケティング用語集
因子分析
統計学上のデータ解析手法のひとつ。
「因子」は何かの結果を引き起こす原因を意味する。つまり因子分析とは、たくさんの結果(変数)の背後に潜んでいる要因を明らかにすることだと言える。マーケティングの現場では、アンケート調査の結果を分析し、回答者の「潜在意識」や「隠れた想い」のようなものを見いだす目的で使われる分析手法。
因子分析の成り立ちと考え方
もともと因子分析は教育心理学の分野で、生徒の能力を測定するために開発されたと言われている。生徒の能力を測るために多くの科目テストを行うが、各教科の成績を並べて見るだけでは、各生徒のテスト成績に関して、なぜその成績だったのか、科目によって点数に差があるのはなぜなのか、といった要因は説明できない。
そこで、生徒たちの各教科の成績を全体として分析し、成績の背後に隠れている成績を左右する個人の能力、たとえば読解力、発想力、説明力といった少数の「共通因子」を見いだすことが重要になる。各生徒の成績は、それぞれが持つ共通因子の能力の大小やその組み合わせと、各教科の固有の要因である「独自因子(特殊因子)」によって説明できると考えられる。
これが、因子分析の考え方で、因子分析は当初、心理学の特に知能研究のみに応用できる分析方法だと考えられていたが、今日では経済学や医学など多様な学問にも使われ、ビジネスの現場でも特にマーケティングリサーチの分析で頻繁に活用されている。
<因子分析のモデル図>
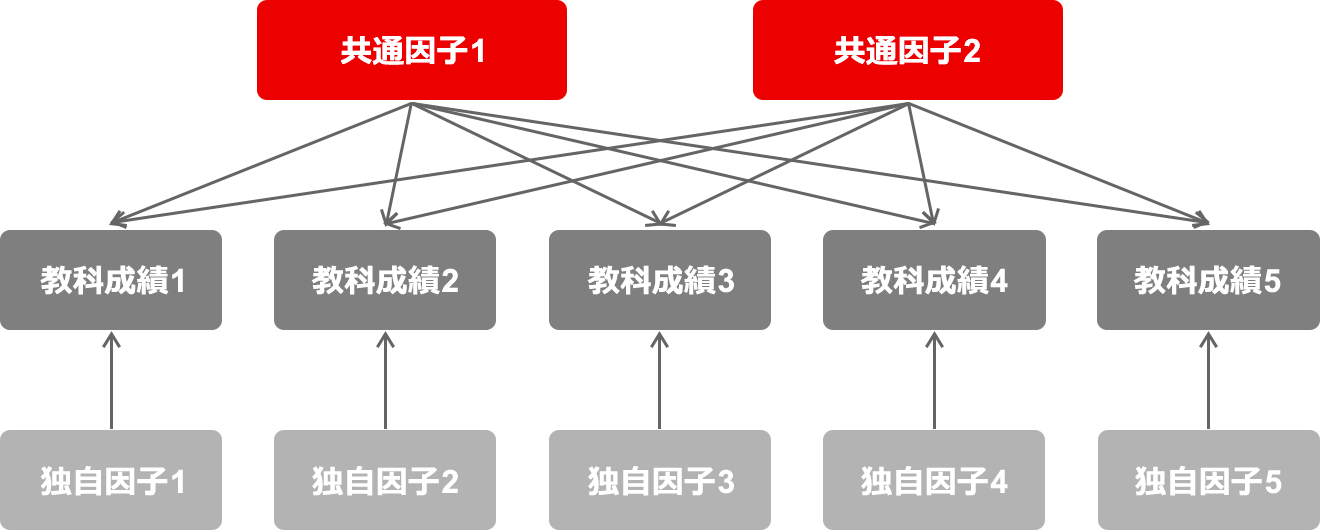
多変量解析における因子分析の位置づけ
因子分析は、複数のデータの関連性を明らかにする統計手法の総称「多変量解析」の一手法で、解析の目的や、扱う対象となるデータの種類によって、他にも数多くの分析手法がある。
多変量解析は大きく分けて、将来の「予測」をするタイプと、数多いデータを「要約」するタイプに分けることができるが、因子分析はデータを要約するタイプに当たる。
因子分析の手順と基本用語
因子分析は複雑な計算を連続で何回も行うため、Excel単体では厳しい。Excelに付加するアドインソフトや、「SPSS」「SAS」「R」といった統計ソフトで行う。その手順について、因子分析は進め方が数々あるが、一般的には以下の手順で進める。
1:共通因子の数を決定
アンケート結果など、分析したいデータから「固有値」を計算する。統計ソフトで変数の数だけ因子1から2、3……と各因子の固有値が算出されますので、それを見て、急激に数値が小さくなる手前までの因子を、分析する価値のある共通因子として決定する。共通因子の数を決定する方法は他にもいくつかある。
【固有値】
固有値とは、各因子の全項目に対する支配度のことで、固有値が大きいほど影響の大きい因子ということになる。
2:因子負荷量の算出
次に共通因子の影響の強さを示す「因子負荷量」を抽出する。抽出方法は多くの種類があり、統計ソフトでは7種類程度用意されていることが多い。どの抽出方法も統計的に間違いではなく、考え方と計算方法の違いである。最も一般的なのは「最尤法(さいゆうほう)」で、他に「主因子法」、「主成分法」などがある。
【因子負荷量】
観測変数(上で出した例では各教科のテストの点数や、各店舗の売上高)に対して共通因子がどれくらいの強さで影響を与えているかを示す数値。
【最尤法】
統計学的には、「観測変数が得られる確率が最大になるような母数の値をその推定値とする手法」。簡単に言うと、結果の数値から確率的に一番尤も(もっとも)らしく思える原因の数値を算出する手法。因子分析の場合、因子負荷量どういう数値であれば、店舗売上高のように既にわかっているデータ(観測変数)がその数値になるのかを計算する。
3:因子負荷量の抽出結果の見方
統計ソフトで因子負荷量(下の表では1.16250といった数値)を抽出すると、下記のような項目が算出される。どういう意味のある項目なのか、簡単に用語を説明する。
<因子負荷量の計算結果例>
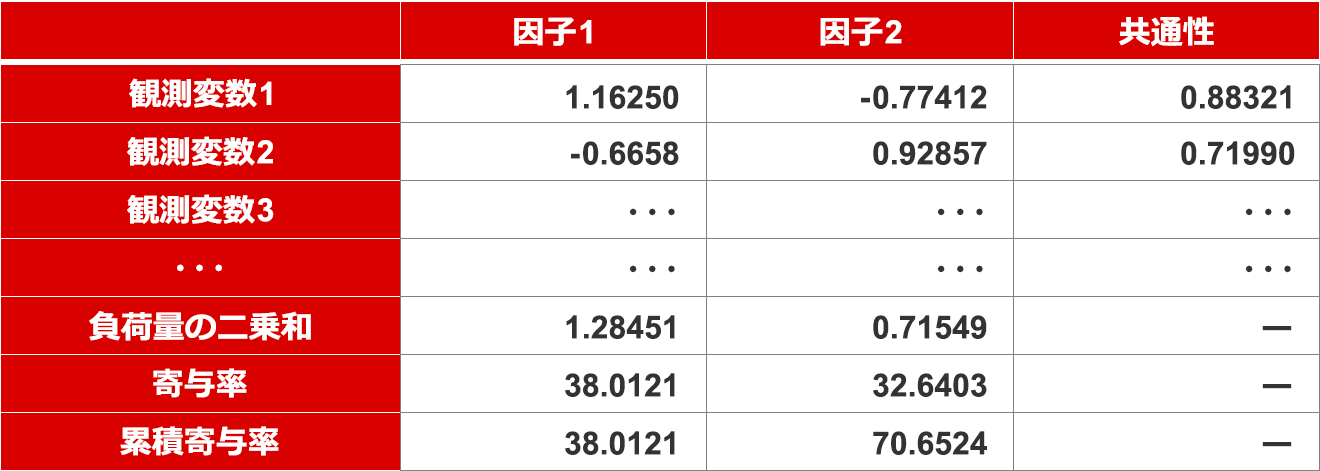
【共通性】
因子群(表では因子1と因子2)によって、各観測変数がどの程度説明できるかを示す数値。0(まったく説明できない)から1(完全に説明できる)の間の値。1ー共通性=独自因子の分となる。
【負荷量の二乗和】
因子寄与と呼ばれる数値。その因子がすべての観測変数に対して、どれくらい寄与(影響)しているかという指標。この数値が大きいほどその因子の影響が大きいと言える。上の例では因子1のほうが因子2より影響が大きいことになる。
【寄与率】
因子寄与の合計は観測変数の総数と同じ。そこで、因子寄与を観測変数の総数で割ることで、その因子が全体に対してどれくらい寄与(影響)しているのかがわかる。その数値を寄与率といい、単位は%。
寄与率(%)=因子寄与(負荷量の二乗和)÷観測変数の総数×100
【累積寄与率】
寄与率を左から順に合計した数値。これによって、それまでの因子で全体をどれだけ説明しているかという割合を示す。
4:因子軸の回転
各観測変数の因子負荷を散布図グラフにすると、そのままでは共通因子が何を指しているのかわかりにくい場合が多いので、解釈しやすいよう、グラフの軸を、各因子の数値が軸に沿って位置するように回転させる。具体的には統計ソフトで数値を変換するのだが、回転の計算方法にも多くの種類がある。以前はバリマックス法が一般的に使われていたが、現在ではプロマックス法がよく使われる。
<因子軸の回転のモデル図>
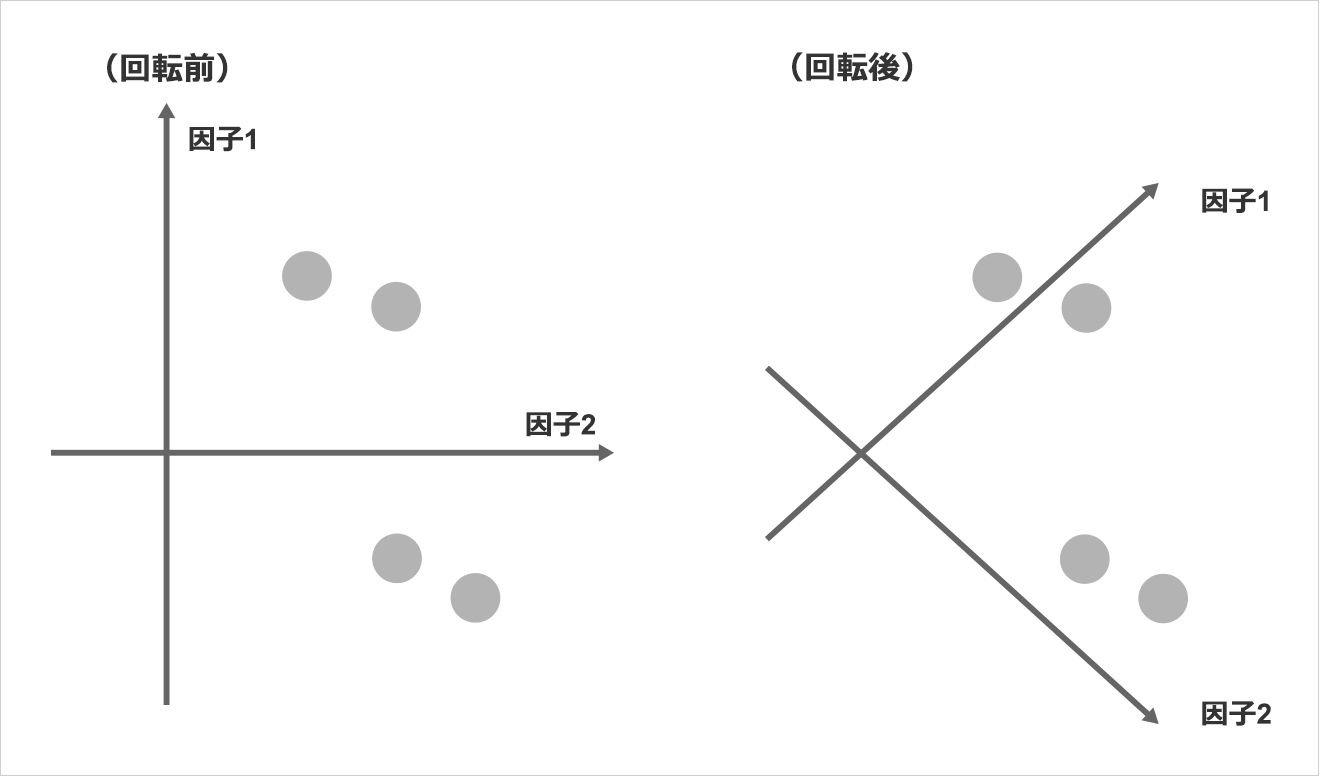
5:因子の解釈
回転によって解釈しやすくなったところで、共通因子名を決める。上の学力の例で出した読解力、発想力、説明力など。これは決まった答えがあるわけではないので、分析者の主観になる。
6:因子得点の算出
各アンケートの回答者や回答者のクラスタ(階層、グループ)の特徴を分析したい場合、因子得点を算出。因子得点によって、共通因子から見た各回答者の能力や資質や好みなどが推測できる。
【因子得点】
各調査対象者が各共通因子にどれだけ持っているかを表す数値。計算方法としては、「回帰法」や「バーレット法」などがある。
因子分析の活用事例
最後に、因子分析をマーケティングに活用した事例を紹介する。
○調査背景
ドラッグストアチェーンのA社では、化粧品コーナーの販売額が落ち込んでいた。今まではどの店舗もほぼ同じ売場構成で品揃えもほぼ同じだったのだが、来期は予算をかけて化粧品コーナーのリニューアルを行うことになった。
A社の店舗はビジネス街、大学の近く、スーパー内など、特徴ある店舗が多かったため、店舗クラスタによって求めているものが違うのではないかという仮説を立て、女性の「化粧品購入の意識」をテーマに、アンケート調査を行うことになった。
○調査項目
アンケートの調査項目は下の9つを設定し、質問項目に「非常にそう思う」から「まったくそう思わない」までの5段階の尺度で選んでもらった。
(1) 夜の肌の手入れに時間をかけたい
(2) 美白化粧品は長く続けないと効果がない
(3) 若いとき美容液を使いすぎると肌によくない
(4) 医薬部外品はふつうの化粧品より効果が高い
(5) ディスカウントで値引き率の高いのは品質が不安
(6) 科学的な肌の診断をしてくれる化粧品メーカーは信頼できる
(7) 大手メーカーのものは安くても安心
(8) 化粧水などよく使うものは安いほうがよい
(9) 値段に関係なく気にいったものを買う
○共通因子を3つに決定
アンケート結果を統計ソフトで分析した結果、女性が化粧品を購入する背景として、3つの共通因子を決めた。そして、アンケート質問との関連を見て、次の3つだと推測した。
第1因子:「肌手入れ」重視
第2因子:「化粧品知識」重視
第3因子:「低価格」重視
○クラスタ別の因子得点を算出
次に、アンケート回答者ごとの因子得点を算出し、回答者を「学生」「ビジネスパーソン」「専業主婦」のグループに分けて、各グループの因子得点の平均値をグラフにしてみた。
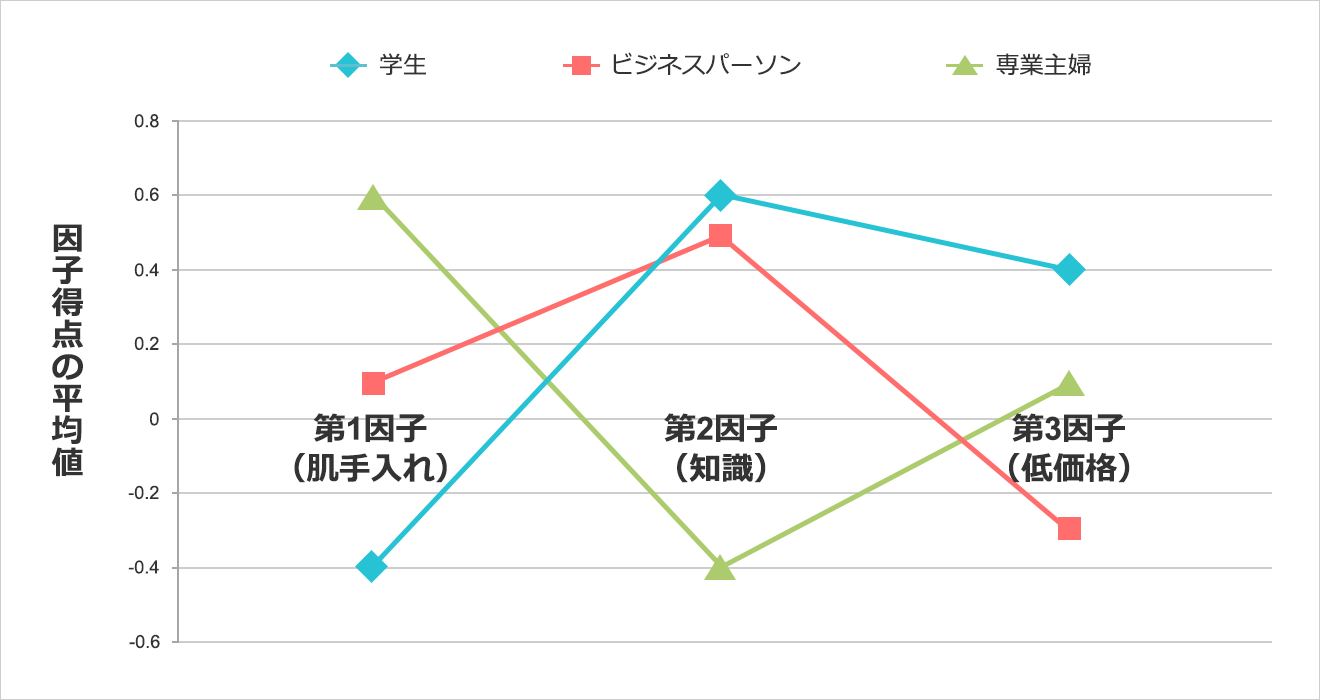
- 学生 … 知識(第2因子)と低価格(第3因子)の得点が高く、商品知識を求め、低価格志向
- ビジネスパーソン … 知識(第2因子)が高く、学生と比較すると、低価格へのこだわりは低い
- 専業主婦 … 肌手入れ(第1因子)が高く、肌の手入れに熱心。価格も多少重視
ということが推測できた。
○分析結果を活用
売場改革は、それぞれ店舗の顧客層を考え、街中のビジネスパーソンが多い店舗では商品解説のPOPやモニタでの動画解説を増やし、メーカーの研究員出身など商品に詳しい社員を配置することになった。スーパー内など専業主婦が多い店舗ではサンプル品を多く置き、実際に試せるスペースを設けることになった。大学に近く学生が多い店舗では現在より低価格商品の品揃えを増やし、他の店の型落ち在庫品なども集中的に回すことが決まりった。
アンケートの因子分析の結果を活用し、A社の売場は大きく変わり、化粧品コーナーの売り上げは伸びたことだろう。
因子分析は「多変量解析」の一手法
因子分析は、マーケティングにおいて頻繁に使われる「多変量解析」のための分析手法のひとつ。多変量解析とは、複数の変数を持つデータの関連性を明らかにする統計手法のことで、因子分析以外にも、多くの分析手法がある。解析の目的や、扱う対象となるデータの種類によって、表のように分類できる。
●多変量解析の主な分析手法
|
分析の目的 |
目的変数 | 説明変数 | |
| 量的変数 | 質的変数 | ||
|
予測 |
量的変数 |
|
|
| 質的変数 |
|
|
|
|
要約 |
なし |
|
|
多変量解析の目的は大きく分けて、購入率、売上や当選率など何らかの結果を「予測」することと、学校の試験結果を文系と理系に集約するなど「要約」することの二つに分けられる。さらに扱うデータが数字による量的変数か、性別などの数字ではない質的変数かによって解析手法が異なる。
それぞれを簡単に解説する。
重回帰分析
複数の量的な説明変数から、一つの目的変数を予測する手法。たとえば、店舗面積・従業員数・商圏人口・広告費から、来客数を予測するといった分析。
数量化Ⅰ類
基本的には重回帰分析と同様ですが、質的変数から量的変数を予測する分析手法。たとえば、性別、飲酒の有無、喫煙の有無、運動の有無から、癌になる確率を予測するといった分析。
判別分析
上の数量化Ⅰ類と逆で、量的変数から質的変数を予測し、1か0のグループ分けをする手法。たとえば、B2Bビジネスにおける見込み客の企業規模・従業員数・売上高・利益率から、契約/非契約を予測するといった分析。
ロジスティック回帰分析
判別分析と似ていますが、1か0かを判別するのではなく、目的変数が1となる確率を予測する手法。たとえば、見込み客の企業規模・従業員数・売上高・利益率から、その見込み客が契約する確率を予測するといった分析。
数量化Ⅱ類
判別分析と同様、グループ分けする分析手法ですが、質的変数から質的変数を予測する。たとえば、性別、飲酒の有無、喫煙の有無、運動の有無から、癌になる/癌にならないなどの予測をするといった分析。
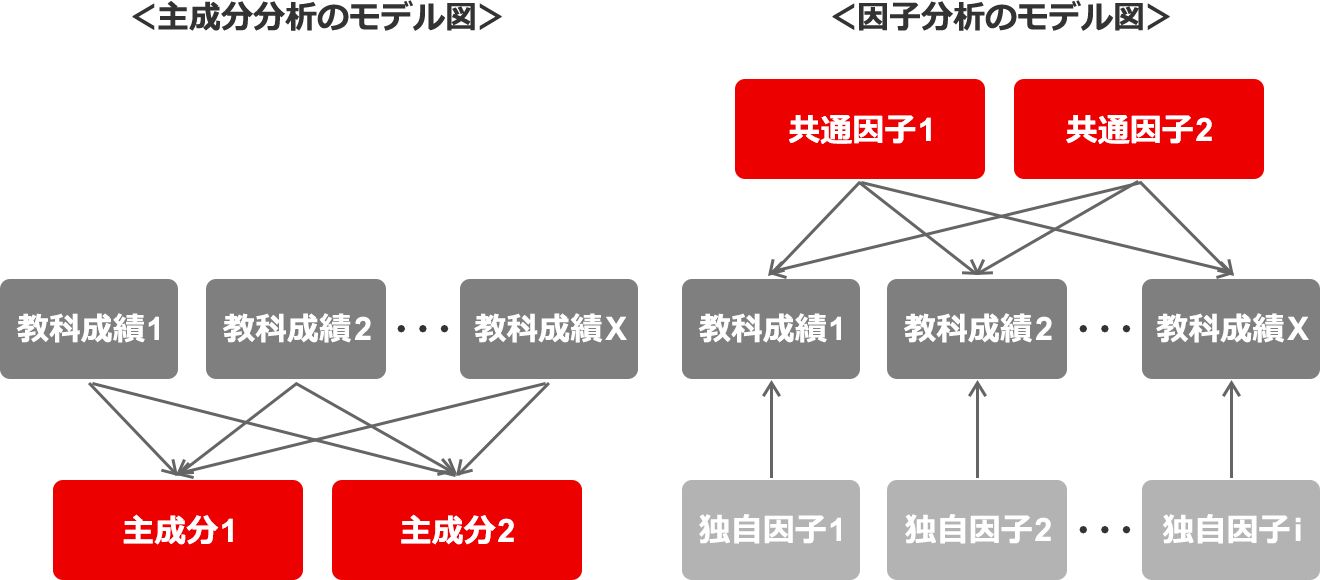
主成分分析
複数の量的な説明変数を、より少数の主成分という指標(合成変数)に要約・集約する分析手法。たとえば、学校で10科目の試験を行った際、第1主成分で総合得点という1つの指標に要約し、第2主成分で文系得点/理系得点という2つの指標に要約するといった分析。
因子分析
主成分分析は複数の説明変数を素に、少数の変数を作成しますが、因子分析は複数の説明変数に影響を与えている共通因子を抽出する分析手法。たとえば、学校の10科目の試験結果のうち、現代国語と古文と論文の成績が良いのは、文系因子が高いからだと説明するといった分析。
クラスター分析
異なる性質の人や物が数多く集まっている集団から、何らかの視点で似た性質のクラスター(集団)を集め、グループ分けする分析手法。たとえば、従業員アンケートの結果から、マイペース型と集団型を分けたり、ファッション感度の高いクラスターを抽出したりするといった分析。
数量化Ⅲ類
主成分分析と似た手法で、複数の質的な説明変数から少数の変数へと要約する分析手法。たとえば、顧客アンケートを元に、商品やブランドのポジショニングを分類するといった分析。
コレスポンデンス分析
数量化Ⅲ類と同様の手法で、クロス集計表などの量的な説明変数を用いたものを指す。たとえば、顧客アンケートの結果をクロス集計して、商品やブランドのポジショニングを分類するといった分析。
因子分析と主成分分析の違い
多変量解析の中で、因子分析と同じくデータを要約するタイプに「主成分分析」がある。多くの統計ソフトでは、因子分析の計算時、主成分分析がオプションとして組み込まれているほど関連の深い分析方法。
下の図でわかるように、因子分析はテストの点数の原因(因子)を見いだす手法で、主成分分析はテストの点数から合成した指標(主成分)を作り出す手法。因果関係が正反対で、考え方も計算方法も違う。
特に実務上で違いが大きいのは、主成分分析は主成分1が「総合評価」で主成分2以降よりも序列が上になるが、因子分析で見いだされた共通因子は特に序列はないということ。また、データの誤差に対する扱いも違う。主成分分析は誤差を認めないか誤差を含んで分析し、因子分析は誤差を独自因子として共通因子とは分けて分析する。
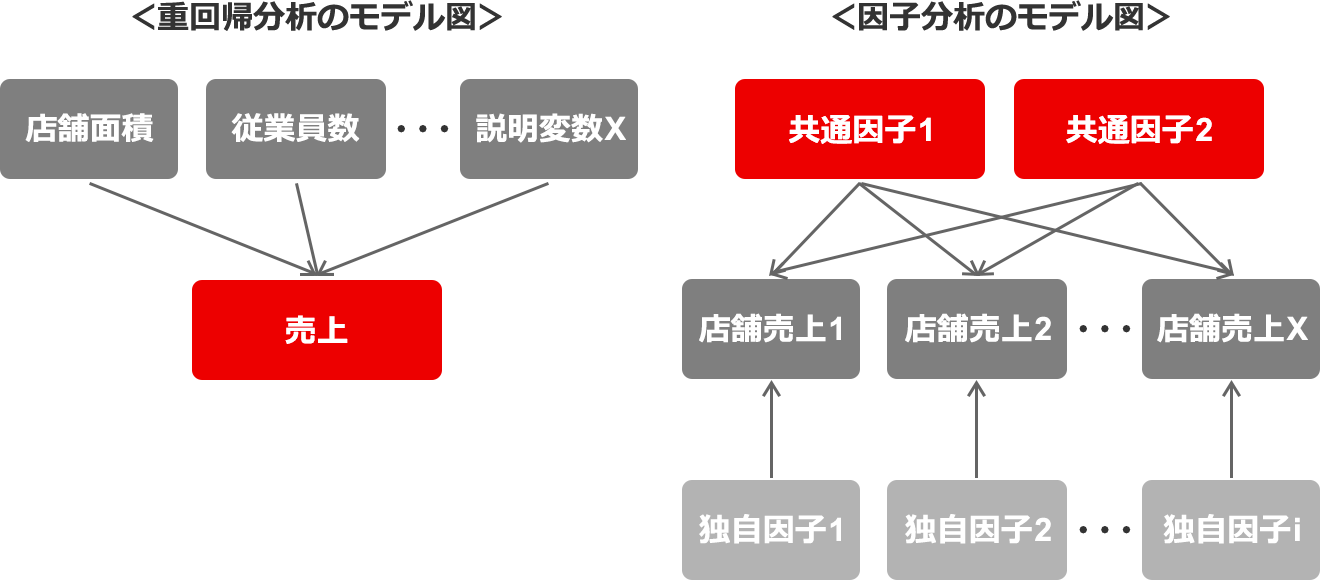
因子分析と重回帰分析の違い
もうひとつ、多変量解析の中でビジネスに活用されることの多い「重回帰分析」と因子分析の違いも説明する。重回帰分析は、判明しているデータから、将来の数値を「予測」するタイプの代表的な分析手法。
たとえばチェーン店において、既存店の売場面積、従業員数、販売商品数、駐車場の収容台数、駅からの距離など複数の要因が、売上高という結果をそれぞれどの程度決定づけているのか分析し、出店予定の新店舗の売上高を予測するといった場合に利用される。
さきほどの例を因子分析で分析する場合には、既存店の売上高を集め、そこから売上高の大小を説明できる共通因子を見いだすという順番なので、考え方が大きく違う。分析目的によって使い分けることで、より深くより広く分析できる。
※解説に使用しているデータ、図版はダミー
