マーケティング用語集
多変量解析
ある対象から得られたお互いに関連のある多種類のデータ(変数、変量)を総合的に要約したり、将来の数値を予測したりといった解析作業の総称。
多変量解析は、特定の分析方法を指すわけではなく、重回帰分析やクラスター分析など、数多くの分析方法が含まれる。
マーケティングにおいては、顧客数や商品単価、店舗数などから将来の売上高を予測したり、何十万ものID-POSの販売データから顧客を特性が似たグループに分けたりといった目的で頻繁に活用されている。
目次
多変量解析でできること
多変量解析は、統計学的には「多くの情報を基にその関係性を解き明かす」手法である。しかしビジネスで活用する際には、「データを使って複雑な問題を解決すること」が求められている。
- チェーン店で、既存店舗の売上高や顧客数、顧客単価、商圏人口などのデータから、「もしこの土地に店舗をオープンさせたら、将来的な売上はいくらになるのか知りたい」
- 消費者アンケートの結果から、「自社の商品は競合と比べて、どこが強みで、どこが弱みなのか知りたい」
- 食品の各種含有成分を質量分析した結果から、「人気が高いジュース飲料には共通してどういう成分が多いのか知りたい」
- 身長や体重、体脂肪率、肺活量、血圧などのデータから、「病気の有無や、その確率を知りたい」
こうした例からわかるように、多変量解析は実践的な手法と位置づけられている。
1変量解析と2変量解析
多変量解析は多数の変数から分析するが、最初から複雑な多変量を扱うのは難しいものである。そこで、先に「1変量解析」や「2変量解析」を行って、データの構造や特質を理解した上で多変量解析を行うことが、データ分析成功の基本とされている。
1変量解析
単変量解析とも呼ばれ、1つの変数だけを取り上げて解析することを言いう。たとえば、過去のさまざまな業績数字の中から、売上高だけ、顧客数だけなど、1要素だけを見て分析を進めること。平均や中央値といった数字で分析を行うことも可能ですが、数字だけを見ていてもわかりにくいので、通常はヒストグラムや箱ひげ図で視覚化して分析する。
・ヒストグラム
データの散らばりを視覚化できるグラフで、度数分布図や柱状グラフとも呼ばれる。
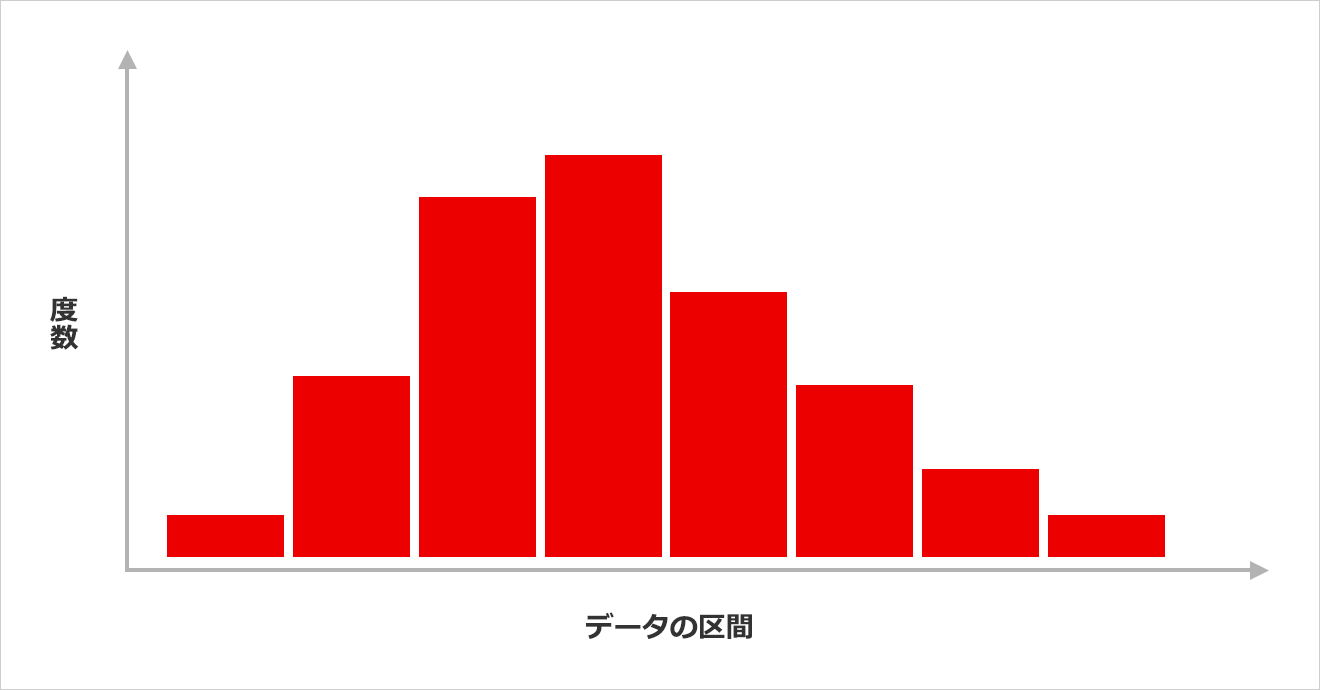
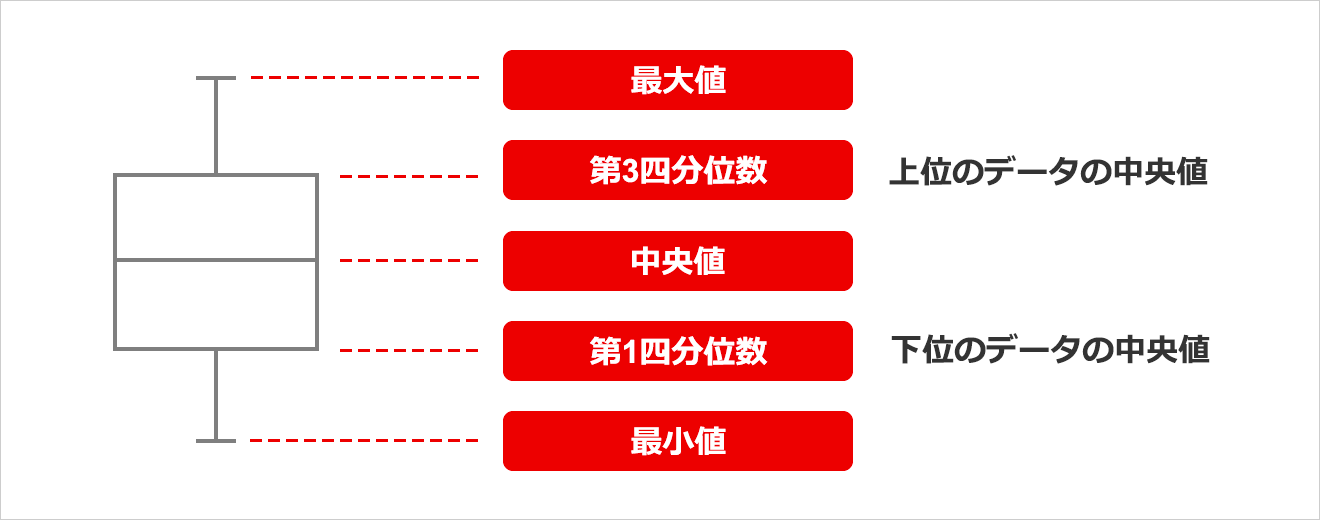
・箱ひげ図
データのばらつきをわかりやすく視覚化するための図。数値の真ん中から上下25%ずつを囲った箱と、箱からのびる線(=ひげ)で表現。ちなみに、似通った図は株価チャートで用いられるが、株価チャートでは箱の上下が始値・終値を示し、ひげの上下が高値・安値を示しており、箱ひげ図とは示すものが異なる。
2変量解析
2つの変数で解析することを「2変量解析」と言う。たとえば、売上高と顧客数、売上高と顧客単価の2項目を同時に解析すること。2変量解析では、通常、相関係数を求めて分析を行うが、視覚化としては散布図、そしてクロス集計表もよく用いられる。
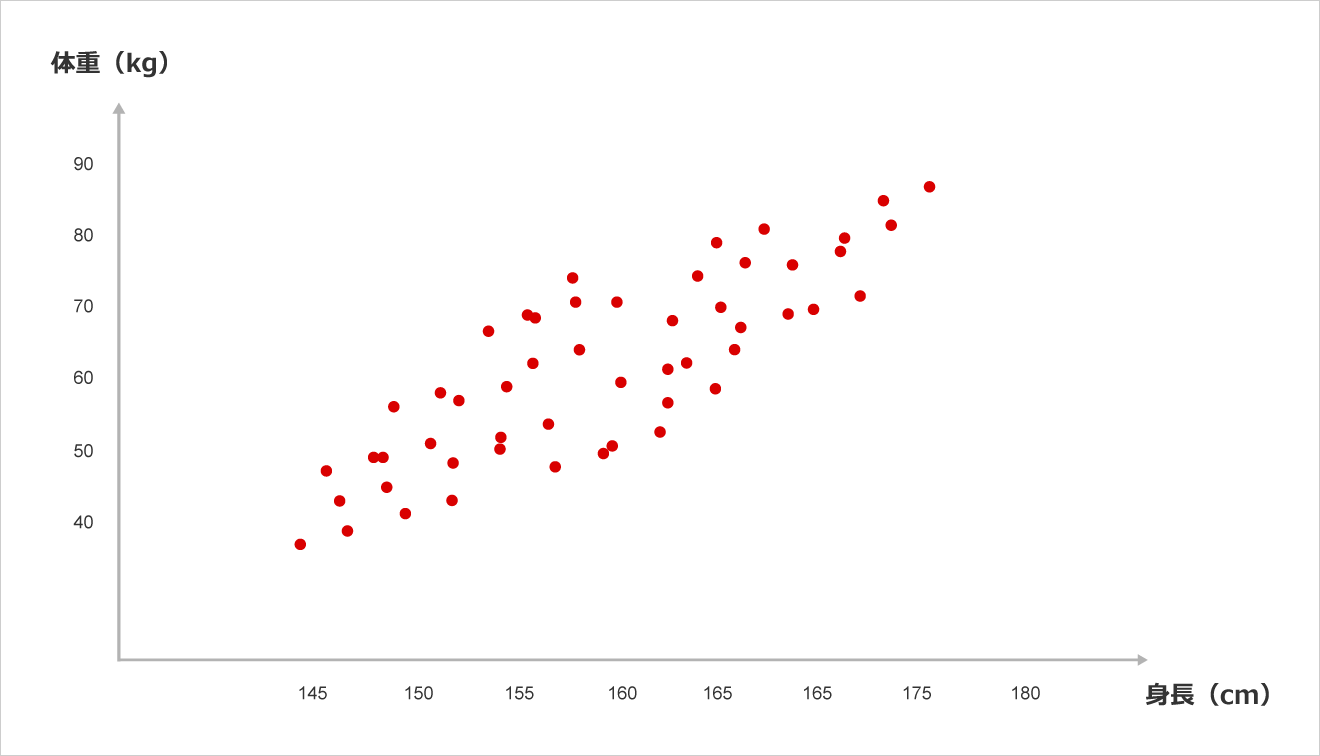
・散布図
縦軸と横軸に2変数の量や大きさ等を対応させて、データを点で打ったグラフ。 変数の散らばりや集まりを視覚化することで、データの特性や傾向などがわかりやすくなる。異常値や外れ値も一目でわかる。
多変量解析での分析の手順
多変量解析は、以下のステップで進める。
| データ収集 | 対象データ選択1/0変換(質的→量的変換) ※必要に応じてデータクリーニング |
|---|---|
| 1変量解析 | 外れ値、異常値の処理図による分布状況確認時系列分析 ※必要に応じて |
| 2変量解析 |
クロス集計分析散布図による分布状況確認
|
| 多変量解析 |
経営課題を多変量解析で分析することが決まったら、最初にどういう目的で、どういう活用をするために分析するのかという分析設計を行う。最初に活用のことまで考えておくことで、どういう調査が必要か、どこまでの精度が必要かといった条件が明確になる。
そして調査・データ収集が終わったら、分析対象とするデータの選択も重要。試行錯誤できるよう、少し広めに選択しておく。分析するデータは、データクリーニング(データクレンジング)する。基本は「重複の削除」「欠損値や異常値の処理」。必要であれば、質的データを量的データに変換(1/0変換)。アンケート質問の「購入の有無」「好き・嫌いの5段階評価」など数量で答える質問ではないデータを数値化することである。
その後、「1変量解析」「2変量解析」を行って、異常値や外れ値を修正・削除し、対象データを再検討する」といった予備分析を行う。
そして、多変量解析に進む。実際の分析作業はコンピュータで行う。ソフトはExcel(エクセル)単体で分析できる場合もあるが、多くはデータ量や計算回数の問題で、Excelでは対応しきれません。その場合、Excelに付加する「エクセル統計」などのアドインソフトや、フリーの統計ソフト「R」、有料でパワフルな「SPSS」「JMP」といった統計ソフトで行う。
分析が終了したら、結果を充分に解釈して、実際のビジネスに活用していく。
多変量解析の目的
多変量解析を行う目的は、大きく分けて2つある。
1)予測
現在の売上高・顧客数・顧客単価・商品別売上高など各項目の過去からの推移を要因とともに分析、将来の売上高を予測するといった目的。売上予測だけでなく、顧客数予測、顧客単価予測、商品別売上高予測など、さまざまなマーケティング予測に活用できる。各要因が結果にどの程度影響を及ぼしているのかという関係を数式で表せることもあり、さまざまな応用が可能。
なお、リサーチでは、予測する目的である「将来の売上高」を「目的変数」、予測のために使う「顧客数」などの項目を「説明変数」と呼ぶ。
2)要約
要約とは、生活者の購入商品決定のメカニズムや、市場の特性など、複雑でさまざまな要素が絡む事柄を、わかりやすく単純化すること。たとえばマーケティングリサーチで聞く何十問もの回答結果はそのまま理解するにはデータが多すぎるため、なるべく元データの情報を損なわないよう、回答の傾向を探ったり、回答者をグルーピングしたりという形で要約する。
要約は、データの解釈自体が目的なので、「目的変数」はない。
多変量解析を行う場合、目的が予測か要約のどちらかによって、分析する手法が変わる。
多変量解析で使用するデータの種類
もうひとつ、多変量解析をする際に分析手法を決める要素に、「データの種類」がある。量的データと質的データに分けた上で、さらに2つずつ、計4つに分けられる。
量的データ
数値で表せるデータのことで、「数量データ」「定量データ」とも呼ばれる。売上高、店舗数、販売数など。以下の2つに分けることができる。
1)間隔尺度
基準となる単位があり、差に意味があるデータ。温度や年号などがあたる。たとえば気温が10℃から20℃に上がったといった差は測定できるものの、2倍に暑くなったとは言えない。
2)比例尺度
間隔尺度の中で、絶対原点(基準点、絶対零点)があり、比に意味があるデータのこと。金額、距離、重量などがあたる。数値の差とともに、数値の間隔や比率にも意味がある尺度。たとえばセールで1,000円の商品が900円になった場合と、10,000円の商品が9,900円になった場合では、どちらも100円OFFだが、前者は10%OFFで、後者は1%OFFとなり、数値の比率が意味を持つ。
質的データ
数値で表すことができないデータのことで、「定性データ」「カテゴリーデータ」とも呼ばれる。たとえば「好き・嫌い」「買う・買わない」といったデータ。こちらも2つに分けられる。
3)名義尺度
単に各データを区別し、分類するための尺度。性別、血液型、居住地、職業などがあたる。数字の大小には意味がない。
4)順序尺度
順序や数値の大小には意味があるものの、間隔が等しいとは限らない尺度のこと。順位や好き・嫌いなどがあたる。たとえば営業成績は1位・2位・3位と順序付けができ、順位数字の大小にも位置があるが、1位と2位、2位と3位の営業数字の差は同じではないなどの例が挙げられる。
ただ実際には、アンケート調査の回答などで、「嫌い=0、普通=1、好き=2」として、順序尺度(質的データ)を間隔尺度(量的データ)に1/0変換して使うことも一般的。
多変量解析の種類と選択方法
多変量解析にはさまざまな分析手法が含まれるが、目的が「予測」か「要約」か、目的・説明の両変数が「量的データ」か「質的データ」かによって、ある程度絞られる。下の表の各欄に複数の分析手法がある場合も、考え方による計算方法が違うといった場合が多いため、選びやすい。
●多変量解析の主な分析手法
|
分析の目的 |
目的変数 | 説明変数 | |
| 量的変数 | 質的変数 | ||
|
予測 |
量的変数 |
|
|
| 質的変数 |
|
|
|
|
要約 |
なし |
|
|
以下、それぞれ、主な分析手法を紹介する。
変数を総合化する分析手法
重回帰分析
複数の量的な説明変数から、1つの量的な目的変数を予測する分析手法。たとえばスーパーで来店者数、気温、広告費、購入品数などから、ビールの売上はどの変数との関連が強いのかを分析し、将来の数値や多店舗での数値を予測。予測の精度がどの程度高いのかを算出することもできる。多変量解析の中でも最も使われることの多い分析手法。
判別分析
複数の量的変数から質的変数を予測し、1/0のグループ分けという形で総合化する手法。たとえば、契約中のユーザーの支払金額、支払単価、使用量、契約年数などから、継続/解約を予測。
主成分分析
複数の量的変数を、より少数の主成分という指標(合成変数)に総合化する分析手法。たとえば、企業が自社の店舗に対する満足度調査を行い、生活者に接客の質、品ぞろえ、施設の清潔さなどについて5段階評価をしてもらい、その結果を元に店舗の総合的な満足度などを分析する。
因子分析
主成分分析に似た手法で、因子分析は複数の量的変数に共通して影響を与えている因子を抽出する分析手法。たとえば、主成分分析同様の満足度調査の結果から、どういう因子が満足度に対して影響を与えているかを分析。
変数間の距離を測る分析手法
クラスター分析
さまざまな性質の人や物の集団を、何らかの類似性を元にグループ(クラスター)分けする分析手法。たとえば、従業員アンケートの結果からマイペース型と集団型を分けたり、会員顧客をファッション感度の高さでいくつかのグループに分けたりといった分析を行う。
多次元尺度法
「多次元尺度構成法」「MDS」とも呼ばれる。分析する対象群を類似性の高さに応じて、似ているものを近く、似ていないものを遠くに配置することで、2次元に置き換えてわかりやすくする手法。競合を含めたブランドのポジショニング分析によく使われる。
質的データを扱う分析手法
数量化Ⅰ類
考え方は重回帰分析と同様ですが、質的変数から量的変数を予測する分析手法。たとえば健康に関して、性別、飲酒の有無、喫煙の有無、運動の有無といった質的データを「1/0」の形に変換して、「癌になる確率」を予測するといった分析。
数量化Ⅱ類
考え方は判別分析と同様ですが、質的変数から質的変数を予測。たとえば健康に関して、性別、飲酒の有無、喫煙の有無、運動の有無といった質的データを「1/0」の形に変換して、「癌になる/癌にならない」を予測するといった分析。
数量化Ⅲ類
主成分分析と似た手法で、複数の質的変数から少数の変数へと要約する分析手法。たとえば、顧客へのアンケート調査の結果を元に、質問間や顧客間での類似度を得点化し、ポジショニングマップを作成するといった分析。
コンジョイント分析
生活者がさまざまな条件を考えて総合的に購入商品を選ぶ際、それぞれの条件がどの程度、購入に影響を与えているかという度合い(効用値)を算出する手法。「コンジョイントカード」と呼ばれる専用のカードを使って調査が行われる。 たとえばノートパソコンの新商品開発のためにコンジョイント分析を行う場合、CPUの処理速度や画面サイズ、重さ、価格などの諸条件を「結合(コンジョイント)」した新商品候補が書かれたカードを複数用意し、どの順番で買いたいかを回答者に選んでもらうことで、どの条件がどの程度重視されているかという効用値を出して分析することができる。
